Newtonian mechanics explains the forces involved in wakeboarding and water skiing across water when pulled forward by a motorboat.
The physics is the same for both.
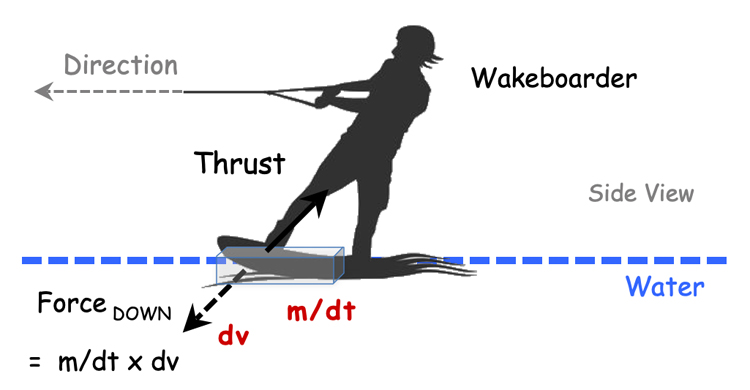
As the board moves through the water, it accelerates a mass of water each second (m/dt) to a velocity (dv) diagonally down and forwards to create a force (Force DOWN = ma = m/dt x dv).
The reaction is an equal and opposite force (Thrust) that pushes the board back and upwards.
This process transfers momentum from the board to the water to push the water down (see illustration below).
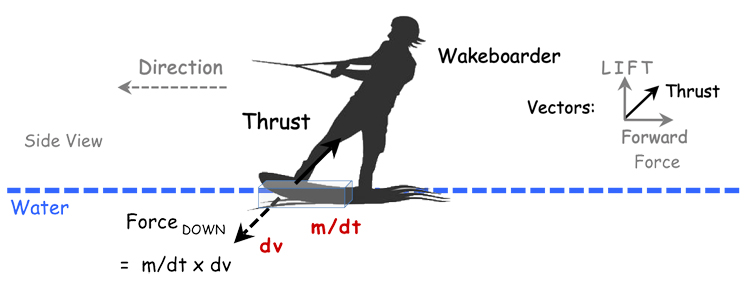
As long as the vertical component (vector) of the thrust created is sufficient to push the board's mass upwards against gravity, then the board flies across the water.
This paper is significant because it provides a novel application of accepted physics and new insights into wakeboarding.
1. Introduction
A. Background
At present, there is no accepted explanation for the physics of wakeboarding across the water.
Some explanations simply state that at a high enough speed, the pressure under the board is sufficient to support the wakeboarder's weight on top of the water.
This statement is correct, but it is not a complete explanation and does not accurately clarify why there's an increase in pressure under the board.
Newtonian mechanics based on the mass flow rate provides a new approach to explaining the physics of wakeboarding.
B. Newtonian Mechanics
The thrust generated (Thrust = m/dt x dv) can be analyzed separately between 'm/dt' and 'dv.'
The vertical force (lift) required by the wakeboarder to stay afloat is constant and does not vary with the speed of the wakeboarder.
For example, the wakeboarder can vary the board's speed and AOA to adjust the 'm/dt' and 'dv' generated and, consequently, the thrust generated.
A slow or stationary wakeboard would simply sink under the water's surface.
In this case, the wakeboard has little momentum and generates insufficient thrust. In turn, this means that there is not enough lift generated for the wakeboard to fly across the water.
2. Newtonian Physics
A. Thrust = m/dt x dv
According to Newtonian mechanics, the part of the wakeboard that has a positive angle-of-attack (AOA) and is in contact with the water can create a force.
As the board moves through the water, it accelerates a mass of water each second (m/dt) to a velocity (dv) diagonally down and forwards to create a force (Force DOWN = ma = m/dt x dv).
The reaction is an equal and opposite force (Thrust) that pushes the board back and upwards (see illustration below).
Where:
m = Mass of water passed through and pushed forward and downward;
m/dt = Mass flow rate;
dt = Change in time (per second);
dv = Change in velocity (v) of the water displaced down;
v = Velocity of the water displaced downward;
a = dv/dt = Acceleration;
Force=ma = mxdv/dt = m/dt xdv;
Force = ma = m x dv/dt = d(m/v)/dt;
Momentum = mv;
The physics described above is summarized by the following equations:
Force DOWN = ma = m/dt xdv (1)
Force DOWN = Thrust (2)
Then equations (1) and (2) can be combined as follows:
Force DOWN = Thrust = m/dt x dv (3)
Or simply: Thrust = m/dt x dv (4)
Units: N = kg/s x m/s
The increase in velocity of the water pushed downward is expressed as 'dv' and not as acceleration ('dv/dt') because it is due to a one-off force (impulse) from the wakeboard.
This action is not time-dependent.
In contrast, the mass of water passed through by the wakeboard is time-dependent and, therefore, is expressed as the mass flow rate (m/dt).
B. The Momentum Theory of Thrust
There is no net gain or loss of momentum, energy, and mass in this process of generating thrust.
The wakeboard transfers momentum and kinetic energy to the water by accelerating the static water passed through diagonally down and forward (see illustration below).
This process can be expressed as the equation:
Force DOWN = ma = d(mv)/dt (5)
Combining equations (2) and (6) allows thrust to be expressed as the change in momentum of the water:
Force DOWN = Thrust = d(mv)/dt (6)
Or simply:
Thrust = d(mv)/dt (7)
Units:
N = (kgxm/s)/s
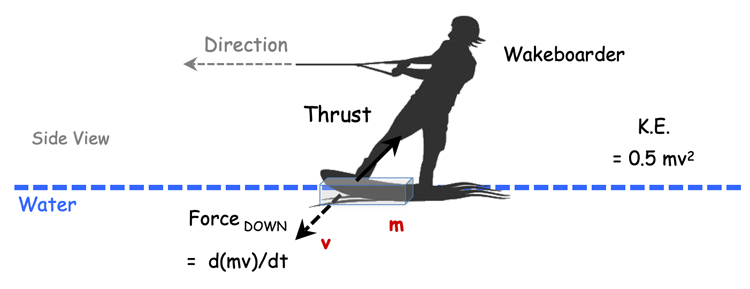
This approach also provides a method to estimate the kinetic energy required to generate thrust, using the standard equation:
K.E. = 0.5 mv2
C. Two Newtonian Equations for Thrust
The analysis above provides two Newtonian methods and equations to calculate the thrust generated:
Thrust = ma = m/dt x dv (mass flow rate) (4)
Thrust = ma = d(mv)/dt (momentum theory) (5)
Both thrust equations (4) and (5) are based on Newton's Second Law of Motion (Force = ma).
Both are correct and produce the same values but express the same thing slightly differently.
According to Newtonian mechanics, a wakeboard cannot generate thrust unless it displaces water downward.
D. Additional Considerations
Board AOA
a) Initially, when moving from a stationary position in the water to moving across the water, a high board AOA is needed to maximize both 'm/dt' and 'dv.' In contrast, at high speeds, a low board AOA is needed to minimize both 'm/dt' and 'dv';
The Time Element of the Thrust Equation
a) The overall acceleration of the water is expressed as 'dv,' and not 'dv/dt,' because this action is due to a one-off force (impact) on each water molecule from the board. The acceleration of each water molecule is not continuous and, therefore, not time-dependent. The acceleration of each water molecule ceases after the impact from the board;
b) Whereas the mass of water involved in this action is time-dependent, so it is expressed as 'm/dt' and not 'm'. The mass of water displaced by the board increases with time;
'm/dt' and 'dv'
a) The mass of water displaced by the wakeboard each second (m/dt) depends on the volume of water displaced and the water density, as shown by the equation:
m/dt = volume/dt x Water Density
For the board in the water:
volume/dt = Surface Area x Board Reach
Surface Area = Width x Length
b) 'm/dt' can be estimated based on the board's surface area that is in contact with the water and "Board Reach";
c) "Board Reach" is the distance away from the board that the board affects the water. It depends on things like the board's speed and AOA;
d) 'dv' depends primarily on the board AOA and speed;
e) 'm/dt' and 'dv' are each presented as a single number in this analysis. But in practice, 'm/dt' and 'dv' vary a lot vertically and horizontally across the board;
Additional Observations
a) The impulse (Ns) is the force exerted by the boards on the water each second;
b) The inertia of the water provides resistance to the backward force. In turn, this inertia allows for the creation of the reactive thrust;
c) A small amount of water is pushed sideways and upwards by the wakeboard. However, this action is negligible to the key forces generated;
3. Discussion of Results
Newtonian mechanics provides a new approach to explaining and understanding wakeboarding and water skiing.
Wakeboards are effectively flying across the water.
It is puzzling that Newtonian mechanics has not previously been applied to explain wakeboarding.
4. Conclusions
Newtonian mechanics based on the mass flow rate (Thrust = m/dt x dv) explains how wakeboards and water skis can fly across the water's surface.
Words by Nicholas Landell-Mills | Author of "Surfing and nose riding explained by Newtonian physics," "The physics of kiteboarding," and "A new theory on sailing downwind faster than the wind"
